Понятие алгоритма.

Для решения задачи исполнителю необходимо указать последовательность действий, которые он должен выполнить для достижения цели - получения результата. Иначе говоря, исполнителю должен быть указан алгоритм решения задачи, представленный на понятном ему языке. Под исполнителем подразумевается как человек, так и вычислительная машина.

Алгоритм решения задачи - это конечная последовательность четко сформулированных правил решения некоторого класса задач.

В обыденной жизни мы постоянно сталкиваемся с алгоритмами как последовательностью действий, приводящих к достижению поставленной цели,- это правила перехода улицы, рецепты приготовления различных блюд, поиск нужного слова в словаре и др. Алгоритмы в математике - это правила нахождения корней квадратных алгебраических уравнений, правила выполнения арифметических действий, правила нахождения наибольшего общего делителя и наименьшего общего кратного, разложение числа на простые множители и др.

Алгоритмы должны обладать целым рядом свойств: дискретностью, точностью, понятностью, результативностью, массовостью.

Дискретность - это разбиение алгоритма на ряд отдельных законченных действий - шагов. Точность - это указание последовательности шагов. Понятность - это однозначное понимание и исполнение каждого шага алгоритма его исполнителем. Результативность - обязательное получение результата за конечное число шагов. Массовость - применимость алгоритма к решению целого класса однотипных задач.

Если бы мы знали алгоритмы решения всех задач, то их исполнение можно было бы поручить машине. Но оказалось, что не все задачи, которые нам хотелось бы решить, имеют алгоритмы решения. Задачи, в принципе не имеющие общего решения, называют алгоритмически неразрешимыми. К примеру, мы знаем, как решить любое квадратное алгебраическое уравнение, пользуясь одним и тем же алгоритмом. Похожие формулы существуют и для кубических уравнений и для уравнений четвертой степени. Но уже для уравнений степени выше четвертой таких формул нет и в принципе быть не может, хотя в частном случае отдельные уравнения можно решить. Есть и другие алгоритмически неразрешимые задачи, например задача о трисекции угла, о квадратуре круга и др.

Существуют различные способы представления алгоритмов. В пособии рассматривается представление алгоритма в виде схем, на языке программируемого микрокалькулятора и на языке программирования БЕЙСИК.

Схема алгоритма. Схема алгоритма представляет собой графическое изображение алгоритма с помощью определенным образом связанных между собой блоков. Под блоком понимается любой конечный этап вычислительного процесса, принимаемый в данной схеме как целое. Типы блоков представлены на рисунке 2. Внутри каждой геометрической фигуры дается описание операций, содержащихся в данном блоке. При этом используются символы математических операций и операций отношений.

Функциональный блок (рис. 2, а) используется для представления функций. В этом блоке осуществляется преобразование информации по заданному действию S. Блок проверки условия
(рис. 2, б) используется для управления преобразованием информации. В результате анализа условия Р выбирается одно из двух возможных направлений "да" или "нет", и управление передается блоку, записанному на выбранном направлении. Информационный блок (рис. 2, в) используется для обозначения операций обмена информации между устройствами. Блоки, изображенные на рисунках 2, г и д, называют соответственно начальным и конечным. Объединяющий блок (рис. 2, е) указывает на передачу управления от входящих стрелок к одной выходящей. Для изображения направления потока управления используются соединительные линии со стрелкой. Алгоритм решения задачи, представленный схемой, начинается в начальном блоке и заканчивается в конечном.

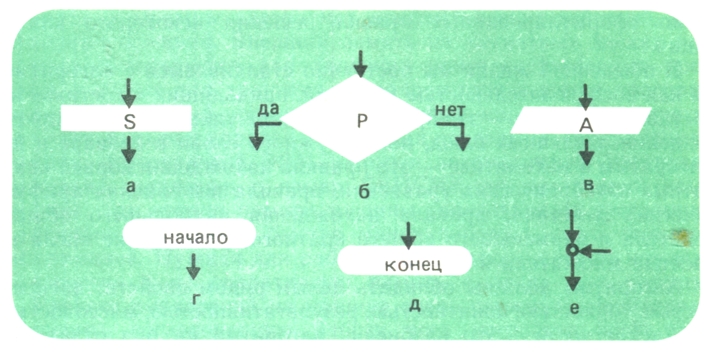
Рис. 2

Базовые структуры. При изображении алгоритмов с помощью схем используются базовые управляющие структуры: СЛЕДОВАНИЕ, РАЗВИЛКА, ПОВТОРЕНИЕ.

СЛЕДОВАНИЕ: структура (рис. 3) означает, что действия S1 и S2 должны быть исполнены одно за другим.

РАЗВИЛКА: действие, определяемое структурой, осуществляет анализ условия Р (истинно или ложно) и альтернативный выбор дальнейшего направления в последовательности выполнения действий в зависимости от значения Р. Различают ПОЛНУЮ РАЗВИЛКУ (рис. 4) и НЕПОЛНУЮ РАЗВИЛКУ (рис. 5). Словесно ПОЛНАЯ РАЗВИЛКА описывается так: если Р истинно, то исполнить S, иначе Т. НЕПОЛНУЮ РАЗВИЛКУ словесно можно описать так: если Р истинно, то исполнять S.

Более сложный язык программирования это ассеблер.